Bevezetés:
Aki rápillant a bejegyzésre és szembetalálja magát a számok és a geometriai ábrák sokaságával, azt azonnal kiveri a víz, az egekbe szökik a hőmérséklete és riadtan nyúl az egér után, hogy fejvesztve iszkoljon el az oldalról. Pedig fölösleges. Mondanivalómat ugyanis alig lesz nehezebb megemészteni, mint egy tic-tacot!
És feltétlenül könnyebben megy majd, mint sárkányt eregetni! Ezért aztán ha egy kicsit is érdekel az aranymetszés és a harmadoló szerelmi viszonyának bűvös titka, biztos lehetsz benne, hogy itt a helyed!
(Annak, akit sért az egyszerű fogalmazás, ami figyelmen kívül hagyja az ő többre érdemes szellemi potenciálját, javaslom inkább A zebra, mint a létezés formáinak kifejezője című hiánypótló tanulmányt.)
Tárgyalás
Minden valamire való szakmának vannak olyan varázsigéi, amelyeket kimondva kiugrik a nyúl a kalapból, mialatt a többi avatatlan néző csak ámuldozva bámulja a csodát. Ilyen varázsszó a fotózásban (és nem csak ott) a misztikus csengésű aranymetszés. Ha vesszük a fáradságot, és utánanézünk a neten, akkor olyan borzalmas levezetésekbe, képletekbe és ábrákba ütközünk, amelyek láttán elmegy a kedvünk még a gyereknemzéstől is. Mint pl. ez:
És feltétlenül könnyebben megy majd, mint sárkányt eregetni! Ezért aztán ha egy kicsit is érdekel az aranymetszés és a harmadoló szerelmi viszonyának bűvös titka, biztos lehetsz benne, hogy itt a helyed!
(Annak, akit sért az egyszerű fogalmazás, ami figyelmen kívül hagyja az ő többre érdemes szellemi potenciálját, javaslom inkább A zebra, mint a létezés formáinak kifejezője című hiánypótló tanulmányt.)
Tárgyalás
Minden valamire való szakmának vannak olyan varázsigéi, amelyeket kimondva kiugrik a nyúl a kalapból, mialatt a többi avatatlan néző csak ámuldozva bámulja a csodát. Ilyen varázsszó a fotózásban (és nem csak ott) a misztikus csengésű aranymetszés. Ha vesszük a fáradságot, és utánanézünk a neten, akkor olyan borzalmas levezetésekbe, képletekbe és ábrákba ütközünk, amelyek láttán elmegy a kedvünk még a gyereknemzéstől is. Mint pl. ez:
Na ez az, amivel mi itt most
nem foglalkozunk!
A dolog ugyanis sokkal egyszerűbb annál, mint amit a képlet alapján gondolnánk!
Minden fotós tudja, hogy a kép valamelyik elemét (mondjuk a főtémát) muszáj az aranymetszésbe helyezni. Aki nem ezt teszi, annak kihullik a haja, képeit a szemétdombra hajítja a kegyetlen utókor, és még a hajléktalan is utánaköp az utcán. Aki viszont hajlandó az aranymetszés oltárán áldozni, arra még a földi életben a Mennyei Paradicsom boldogsága vár, és a védekezés nélküli, mégis biztonságos szerelmi együttlét végkifejletének áldása öleli át napjait.
Szánjuk hát rá magunkat, és lépjünk közelebb a titkot rejtő asztalkához! Ám még mielőtt magába a fiókba bekukkantanánk, ne legyünk restek, hajoljunk a földig és nézzük meg az asztallábat is! Ami pedig nem más, mint egy különleges számsor, amelynek (majdnem) minden eleme azonos az őt megelőző két elem összegével.
Máris hétrét görnyedtünk a fájdalomtól e definíciót olvasván! Hát még ha netán azt is meghalljuk, hogy valami Fibonacci-sorozatról van szó! Ezért ezt inkább meg se halljuk! Mielőtt orvosért kiáltanánk, küldjünk be gyorsan egy fájdalomcsillapítót! Két egyszerű számot:
Minden fotós tudja, hogy a kép valamelyik elemét (mondjuk a főtémát) muszáj az aranymetszésbe helyezni. Aki nem ezt teszi, annak kihullik a haja, képeit a szemétdombra hajítja a kegyetlen utókor, és még a hajléktalan is utánaköp az utcán. Aki viszont hajlandó az aranymetszés oltárán áldozni, arra még a földi életben a Mennyei Paradicsom boldogsága vár, és a védekezés nélküli, mégis biztonságos szerelmi együttlét végkifejletének áldása öleli át napjait.
Szánjuk hát rá magunkat, és lépjünk közelebb a titkot rejtő asztalkához! Ám még mielőtt magába a fiókba bekukkantanánk, ne legyünk restek, hajoljunk a földig és nézzük meg az asztallábat is! Ami pedig nem más, mint egy különleges számsor, amelynek (majdnem) minden eleme azonos az őt megelőző két elem összegével.
Máris hétrét görnyedtünk a fájdalomtól e definíciót olvasván! Hát még ha netán azt is meghalljuk, hogy valami Fibonacci-sorozatról van szó! Ezért ezt inkább meg se halljuk! Mielőtt orvosért kiáltanánk, küldjünk be gyorsan egy fájdalomcsillapítót! Két egyszerű számot:
0 és 1
Ugye, nem is fáj?
Mikor már magunkhoz tértünk az egyszerűség fölötti örömünk okozta megkönnyebbülésből, gyorsan adjuk össze a két utolsó számot! Melyik a két utolsó szám? Hát a nulla, meg az egy! Na jó, persze hogy ez a két első szám is egyben - de hát kekeckedünk vagy számolunk? Szóval az összeadás:
0+1=1
Ezt az eredményt pedig tekintsük megkezdett számsorunk következő elemének. A számsor tehát már így néz ki:
0 , 1 , 1
Adjuk össze megint a két utolsó számot:
1+1=2
Számsorunk szépen bővül, már négy eleme van:
0 , 1 , 1 , 2
Folytassam még? Szerintem ennyi is elég, hogy megértsük az összefüggést: ha mindig összeadjuk a két utolsó számot, megkapjuk a számsor következő tagját. Néhányszor megismételve a műveletet a következőket kapjuk:
0 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34, 55 , 89 ,... stb
(Csak a teljességet keresők kedvéért jegyzem meg: korábban azt írtam, a számsor "majdnem" minden eleme a megelőző két szám összegével egyezik meg. Látható, hogy azért "majdnem", mert az első két szám - a nulla és az egy - előtt már nincsenek további számok, amelyekből levezethetnénk őket.)
A számok egy részét pirossal írtam.Miért? Figyelemfelkeltésül. Élükön ugyanis ott díszeleg a babonás 13-as, amelyről mindenki tudja, hogy elátkozott szám! Bajt hoz ránk, a fogunk megsárgul tőle, és még az öttalálatos lottószelvényünket is kifújja a kezünkből a szél, ha összetalálkozunk vele. Jobb tehát elkerülni. És ugyanúgy óvakodjunk az összes többi számtól, ami mögötte sorakozik! Hiszen nyilvánvalóan rájuk vetül az ördögi 13-as halottidéző árnyéka.
Viszont most, hogy ismerjük a számsorozatot, eljött az idő, hogy válasszunk magunknak csillagot! Vagyis számot a sorozatból. Mivel mi szeretjük minden jóból a legnagyobbat kapni, vegyük az utolsó (nem megbabonázott) számokat:
3 , 5 , 8
Ezek lesznek a mi varázsigéink, amelyekkel elővarázsoljuk a nyulat a kalapból!
(Na jó, ez az egész számcirkusz a 13-as körül mind nem igaz. Csak vicceltem. De akkor is ezt a fenti három számot fogjuk használni...)
Kedves Hölgyeim és Uraim, Mélyen Tisztelt Publikum! Végre elérkeztünk oda, ahol a fényképezőgép nézőkéje kezdődik!
Ha veszünk egy olyan négyzetet, ami 8 x 8 apróbb négyzetből áll, akkor máris tetemre hívtuk a számsorunk bűvös nyolcasát:
Ha veszünk egy olyan négyzetet, ami 8 x 8 apróbb négyzetből áll, akkor máris tetemre hívtuk a számsorunk bűvös nyolcasát:
Ez már akár egy négyzetes képkivágásnak is tekinthető, nem? Játszunk el vele egy kicsit! Hiszen van nekünk még két számunk, a 3 meg az 5! Ugye, emlékszünk, hogyan függenek össze a számaink? Így: 3+5=8. Osszuk hát fel a négyzetet ennek megfelelően, és az osztásnál húzzunk egy függőleges vonalat:
Nem csináltunk mást, mint a négyzet 3/8-adánál húztunk egy függőlegest. Tegyük meg ugyanezt vízszintesen is:
És már meg is érkeztünk! Íme a híres-neves aranymetszés, pontosan a két vonal találkozásánál!
Hogy miért pont ott? Ha ennyire felbuzog bennünk a kíváncsiság, akkor vegyük szemügyre az alábbi képletet:
...és tegyük fel a kérdést: biztos, hogy minden részletét akarjuk mi ennek tudni? Nem elég nekünk annyi, hogy az aranymetszés a két 3/8-nál meghúzott vonal keresztezésénél található? (Lehet, hogy nem. Aki többet is szeretne erről tudni, az olvassa el a CSAK ERŐS IDEGZETŰEKNEK szóló záró fejezetet.)
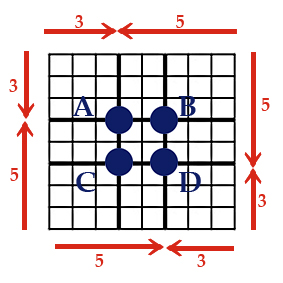
További kérdezősködés helyett most inkább térjünk vissza a négyzetünkhöz! Nem kell sokat gondolkoznunk, hogy belássuk: a négyzet ilyenfajta felosztását továbbfolytathatjuk két újabb vonal meghúzásával:
További kérdezősködés helyett most inkább térjünk vissza a négyzetünkhöz! Nem kell sokat gondolkoznunk, hogy belássuk: a négyzet ilyenfajta felosztását továbbfolytathatjuk két újabb vonal meghúzásával:
Itt tehát már négy pontunk is van az aranymetszésben (A-B-C-D) - ennyi az összes, többet ne is keressünk.
Na most aztán kint vagyunk a vízből! Ki a fene tudja a nézőkén látott képet képzeletben 8 részre osztani, és a 3/8-nál vonalakat huzigálni? Senki!
De szerencsére van egy bűvésztrükkünk, egy cinkelt lap a mandzsettánkban, amivel megoldhatjuk a problémát! Ez pedig nem más, mint a harmadoló! A harmadolás ugyan nem egészen aranymetszés, de majdnem olyan. Jogos a kérdés, hogy miért...
Nézzük csak meg, hogy mi történik, ha 8 x 8 apró kockából álló négyzetünket még egy oszloppal, és még egy sorral kiegészítjük (és hagyjuk benne az egyik aranymetszés helyét is):
Ha rendesen bekockázzuk, nem csak úgy elmaszatolva, akkor egy 9 x 9-es négyzetet kapunk:
Amikor további logikus magyarázattal már nem tudjuk ráirányítani valamire a figyelmet, akkor jön az, amit a matematikusok oly igen nagyon szeretnek. Amikor az egyik ember lát valamit, mert tudja, hogy mit kell látnia, míg a másik, a tudatlan, nem látja, amit a másik lát. Ezen segít a "vegyük észre-metódus".
Lehet, hogy a pokolra kerülök érte, de most én is segítségül hívom az ördög eme csábító kísértését.
Ezért aztán azt mondom: vegyük észre, hogy a 9 részből álló négyzetet a két vonal éppen a harmadánál metszi! Az egyik vonal vízszintesen harmadol, a másik pedig függőlegesen. Végső soron logikus: ha eddig a 3/8-nál volt a metszéspont, akkor most a 3/9-nél lesz. Azt pedig még elemiből tudjuk, hogy 3/9=1/3. Vagyis itt kerül elő nekünk az egyharmad. Más néven a harmadoló!
Ha behúzzuk a többi harmadolót is, akkor minden metszéspontot megkapunk :
Kerüljünk még egy kicsit közelebb a fotózáshoz! A négyzetet alakítsuk át a DSLR-fényképezőgépek 3:2 képarányára (elnyújtva az előző ábrát), és máris úgy érezzük magunkat, mintha lekerültünk volna a lélegeztető gépről:
A fényképezőgép-gyártók szerencsére megteszik nekünk azt a szívességet, hogy láthatóvá varázsolják ezeket a vonalakat, nekünk pedig nincs más dolgunk, mint a metszéspontok valamelyikéhez illeszteni a témánkat.
Ezzel pedig - nem csalás, nem ámítás! - előhúztuk a nyuszit a kalapból! Mert a harmadoló nem egy tökéletes aranymetszés ugyan, de már majdnem az. Olyan, mint a magyar narancs: kicsit hóka, kicsit savanyú, de a miénk. És különben is, gondoljunk bele: ha mi - akik pedig igen okosak és felkészültek vagyunk - nem tudjuk kiszámolni magunkban, hogy hova is esik az a fránya 3/8, akkor az egyszerű ember hogyan tudná? Jó lesz neki a 3/9 is! Ezért aztán veregessük meg a vállunkat, és harmadoljunk bátran!
De azért jobb, ha nem feledjük: ennyi még nem lesz elég ahhoz, hogy mi kapjuk a legnagyobb süteményt!
Befejezés: (CSAK ERŐS IDEGZETŰEK RÉSZÉRE!)
Rettegek a vádtól, miszerint az érthetőség kedvéért kontár módon eltértem a hivatalos matematikai levezetéstől. Ami pedig szigorúan rögzíti, hogy az aranymetszés egy arányosság, amiről akkor beszélünk, ha két rész (a és b) esetén a+b úgy aránylik a hosszabbik részhez (mondjuk a-hoz), ahogy a hosszabbik rész (a) aránylik a rövidebbikhez (b).
Az átlagember ezzel rendszerint jól ki van segítve. Éppen ezért hogy jobban értsük: a bejegyzésben használt példánál maradva aranymetszés esetén a 8:5=5:3. Erről pedig rövid úton meggyőződhetünk, hogy nem igaz! Majdnem azonosak, de mégsem. Az egyik 1,6, másik 1,66. Az aranymetszésre jellemző arányszám pedig se nem 1,6 se nem 1,66 - az igazi érték éppen a kettő között van, kb. 1,618 (és a további tizedesek). Nyilvánvaló tehát, hogy csaltam. Csaltam annak érdekében, hogy érthetővé tegyem az aranymetszést (úgy körülbelül) és azt, hogy a fotózásnál miért áll közel a harmadoláshoz. Ráadásul látható, hogy nem is 3/8-ról kellene beszélnünk, hanem 8/5-ről és 5/3-ról! Na de úgy ki értené meg a hasonlóságot a harmadolóval?
Természetesen az sem véletlen, hogy az említett Fibonacci-sorozatból indultam ki. Ennek a sorozatnak ugyanis csak egyik érdekes tulajdonsága a 3, 5 , 8 számok (és a többi elem) esetében a 3+5=8 jellegű összefüggés (vagyis hogy a 3. elemtől kezdve minden elem az előző két elem összegével megegyező szám), van egy másik csudasága is! Ha elkezdjük a szomszéd elemeket (magyarul számokat) elosztani egymással, akkor ilyesmire lelünk:
5:3=1,6666
8:5=1,6
13:8=1,625
21:13=1,6153
34:21=1,619
Látszólag összevissza ugráló számok. De csak látszólag! Egy koordinátarendszerben ugyanis így néznek ki:
Ezen jól látszik, hogy a hányadosok értéke váltakozva kisebbek, vagy nagyobbak az aranymetszésre jellemző 1,618-nál. A Fibonacci-sorozatból minél nagyobb számokat osztunk el egymással, annál közelebb kerül az eredmény az 1,618-hoz. De ez az eredmény olyan, mint Zorán számában a két kőszobor: sosem éri el! Soha nem lesz a két szám hányadosa azonos 1,618-cal. Hiába no, itt bizony csak az arany(metszés) az, ami fénylik!
Aki tovább szeretné főzni a levest, annak íme a hozzávalók:
Wikipédia - aranymetszés
Wikipédia - Fibonacci-sorozat
Ha behúzzuk a többi harmadolót is, akkor minden metszéspontot megkapunk :
Ezzel pedig - nem csalás, nem ámítás! - előhúztuk a nyuszit a kalapból! Mert a harmadoló nem egy tökéletes aranymetszés ugyan, de már majdnem az. Olyan, mint a magyar narancs: kicsit hóka, kicsit savanyú, de a miénk. És különben is, gondoljunk bele: ha mi - akik pedig igen okosak és felkészültek vagyunk - nem tudjuk kiszámolni magunkban, hogy hova is esik az a fránya 3/8, akkor az egyszerű ember hogyan tudná? Jó lesz neki a 3/9 is! Ezért aztán veregessük meg a vállunkat, és harmadoljunk bátran!
De azért jobb, ha nem feledjük: ennyi még nem lesz elég ahhoz, hogy mi kapjuk a legnagyobb süteményt!
Befejezés: (CSAK ERŐS IDEGZETŰEK RÉSZÉRE!)
Rettegek a vádtól, miszerint az érthetőség kedvéért kontár módon eltértem a hivatalos matematikai levezetéstől. Ami pedig szigorúan rögzíti, hogy az aranymetszés egy arányosság, amiről akkor beszélünk, ha két rész (a és b) esetén a+b úgy aránylik a hosszabbik részhez (mondjuk a-hoz), ahogy a hosszabbik rész (a) aránylik a rövidebbikhez (b).
Az átlagember ezzel rendszerint jól ki van segítve. Éppen ezért hogy jobban értsük: a bejegyzésben használt példánál maradva aranymetszés esetén a 8:5=5:3. Erről pedig rövid úton meggyőződhetünk, hogy nem igaz! Majdnem azonosak, de mégsem. Az egyik 1,6, másik 1,66. Az aranymetszésre jellemző arányszám pedig se nem 1,6 se nem 1,66 - az igazi érték éppen a kettő között van, kb. 1,618 (és a további tizedesek). Nyilvánvaló tehát, hogy csaltam. Csaltam annak érdekében, hogy érthetővé tegyem az aranymetszést (úgy körülbelül) és azt, hogy a fotózásnál miért áll közel a harmadoláshoz. Ráadásul látható, hogy nem is 3/8-ról kellene beszélnünk, hanem 8/5-ről és 5/3-ról! Na de úgy ki értené meg a hasonlóságot a harmadolóval?
Természetesen az sem véletlen, hogy az említett Fibonacci-sorozatból indultam ki. Ennek a sorozatnak ugyanis csak egyik érdekes tulajdonsága a 3, 5 , 8 számok (és a többi elem) esetében a 3+5=8 jellegű összefüggés (vagyis hogy a 3. elemtől kezdve minden elem az előző két elem összegével megegyező szám), van egy másik csudasága is! Ha elkezdjük a szomszéd elemeket (magyarul számokat) elosztani egymással, akkor ilyesmire lelünk:
5:3=1,6666
8:5=1,6
13:8=1,625
21:13=1,6153
34:21=1,619
Látszólag összevissza ugráló számok. De csak látszólag! Egy koordinátarendszerben ugyanis így néznek ki:
A téma szerteágazó, és igazi csemegéje a reál elméknek. Fibonacci-sorozat, Lucas-sorozat, Fibonacci-négyzetek, és -spirálok, megspékelve azzal, hogy a Fibonacci-sorozatot még Bartók zenéjében is fel lehet lelni. Nos és persze a természetben! Hiszen ott vannak a növények, amelyek virágszirmainak száma 5-8-13-21, stb! Hogy az aranymetszés geometriájáról már ne is beszéljünk.
Egyszóval szép dolog ez a matematika! Mert milyen jó például elemi matektudással is megérteni, hogy ha egy kocsmában 4-en üldögélnek és kimegy 8 ember, akkor 4-nek vissza kell mennie ahhoz, hogy senki se legyen a kocsmában!
Bár ez egy marhaság. Egy kocsmában mindig ül valaki...
Egyszóval szép dolog ez a matematika! Mert milyen jó például elemi matektudással is megérteni, hogy ha egy kocsmában 4-en üldögélnek és kimegy 8 ember, akkor 4-nek vissza kell mennie ahhoz, hogy senki se legyen a kocsmában!
Bár ez egy marhaság. Egy kocsmában mindig ül valaki...
-------------------------------------------------------------------------------------------------
Wikipédia - aranymetszés
Wikipédia - Fibonacci-sorozat


















12 megjegyzés:
Jó kis összefoglalót hoztál össze!
2010. szeptember 30. 21:22Érdekes szám ez a 0.618! Annak idején amikor írtam a diplomamunkámat, a helytöltés végett belemerültem az aranymetszésbe és eléggé benne voltam a témában.
Amit számsornak írsz az tulajdonképpen haladvány (így a nulla előtt nem bibis a sor) de ami a legérdekesebb, hogy amit írsz, hogy összeadod a haladvány két számát akkor megkapod a következőt - még furfangosabb! Ugyanis ha ugyanezt a két számot összeszorzod, akkor szintén a haladvány következő számát kapod!
Persze ez csak a FI (0.6180339) szám haladványra igaz.
Szerintem ez a szám nagyon különleges, mivel a természetet "másolja", pl nautilusz csiga hosszában elmetszett háza is tökéletesen követi ezt a növekvő sorozatot - ahogy egyre nő az ívek mérete (akárhova is húzunk bele átlót).
Nemhiába, az ókori görögök ezt már ismerték és törtekkel számoltak, amit ugye tudunk, hogy sokkal pontosabb végeredményt ad, mint a most használt tizedsjegyek!
Ezt holnap elolvasom. Most már túl fáradt vagyok, de érdekel.
2010. szeptember 30. 22:23A Fibonacci-sorozat számaival valóban nagyon jókat lehet játszani, erre több példát is sorolnak a fenti linkek. De ezek megértéséhez már valóban kell némi matematikai véna és elszántság :-)
2010. október 1. 10:22Ezt eddig nem is tudtam, hogy a harmadolás az aranymetszésből indul ki. Hasznos bejegyzés és szórakoztató.:-)
2010. október 1. 10:43Az aranymetszés és a harmadolás összefüggéseiről a Wikipédia is ír a kompozícióról szóló szócikkében, mely szerint a harmadolás 5%-ban tér csak el az aranymetszéstől. Ez pedig olyan kevés, hogy nincs gyakorlati jelentősége.
2010. október 1. 13:13harmadszor próbálom leírni, remélem végre elküldődik...
2010. október 13. 14:42Szóval, már régebben akartam írni, hogy remek ez az összefoglaló, nagyon örülök neki, én is fogom használni még, vagy legalább hivatkozni erre a lapra. Ha nem baj. Mert jó.
Amúgy hihetetlen, hogy még a zene is teljes aranymetszés, egy akkord is így épül fel: dúr akkord esetében a legkönnyebb látni. De a mindenki számára ismert, tipikusan magyar "pentatónia" is erre megy vissza, vagy visszavezethető reá.
Köszönöm Doma. Népszerűsítsd csak nyugodtan :-)
2010. október 13. 15:00Sosem eszméltem rá, pedig milyen igaz: a dúr meg a moll is az aranymetszést követi. Csuda egy dolog ez...
"a zene is teljes aranymetszés, egy akkord is így épül fel: dúr akkord esetében a legkönnyebb látni." – Ha a III-V-VIII hármashangzatra gondolsz, akkor igazad van. Ez egy dúr akkord, ugyanakkor nem szabad megfeledkezni róla, hogy ez egy hátsó inverz dúr (az alaphang a legutolsó, azaz a 8-adik, gyakorlatilag az alaphang terce, kvintje és az oktávja).
2010. december 30. 21:16Mester: nagyon tetszett ez a cikk. Jókat kuncogtam olvasás közben. Pontosan azért, mert a matematikától kihullik a hajam. :) De ez érthető volt.
Mindamellett néhány klasszikus festménnyel lehetett volna szemléltetni az aranymetszés kompozícióját, hogy a földi halandó is megértse, mi a célja ennek a cikknek. Mert annyit felfog, hogy harmadolunk, de odáig már nem jut el, hogy minek? Ezért aztán azt csinálja, hogy vigyázzba állítja a lógó taknyú Pistikét (elnézést minden Pistikétől), aztán az alanyt a kép kellős közepére helyezve, fektetett kivágásban lefényképezi, mert még az sem jut eszébe, hogy mennyivel több információt tartalmazna az a kép, ha mondjuk álló formájú lenne.
Szóval középen ott áll Pistike vigyázzban, a kép két oldalán meg (jó esetben) semmi. Rosszabb esetben a szomszéd ganédombja, disznóólja, lyukas, esővizes műanyag lavórja látszik, amit utólag a Photoshop CS5 igen fejlett Tartalomfüggő-kitöltés effektje segítségével kiretusál a képből. Majd ezt feltölti valami képgagyizó oldalra, mondjuk az imagechefre, rak rá villogó, nyíllal átszúrt szívecskéket, meg egyebeket. És ez a fotósorozat 2359 db tök egyforma képből áll, középpontban Pistikével.
És mindenkinek mutogatja, és örülni kell neki, hogy "de jó már..." Mert ha megmondjuk neki az igazat, akkor csak "tudálékos okostojások" vagyunk, és különben is, a szándékot kell értékelni, meg bla-bla-bla. Biztos ismerős a helyzet.
Szóval néhány klasszikus, aranymetszésben készített festményt (vagy fotót) még be lehetne suvasztani a cikk aljára, kiegészítésképp, hogy "lám, parasztok, erről ugattam egész idáig...!" – vagy valami ilyesmi.
BonFire teljesen igazad van: sok mindennel teljesebbé lehet(ne) tenni ezt a cikket, így például konkrét példákkal az aranymetszés használatáról a művészetben, ahogyan javaslod. Hogy nem teszem, annak nem a makacsságom az oka, hanem az, hogy nem volt célom az aranymetszésről átfogó(bb) dolgozatot készíteni. (Mellesleg már úgyis van belőlük elég.)
2011. január 3. 13:51Ez egy fotós blog - s a bejegyzés megírására a fotós oldalakon tapasztaltak indítottak. Még a kezdő fotósok is hamar megtanulják ezeken az oldalakon az aranymetszés és a harmadolás használatának esztétikai indokoltságát, és rengeteg képi példával is találkoznak. Mégis van némi zűrzavar a fejekben: most akkor aranymetszést kell alkalmazni vagy inkább harmadolni kell, mi a különbség a kettő között, és egyáltalán mi ez az egész? Úgy gondolom, sokan nem tudják, hogy milyen összefüggés van a a címben szereplő két fogalom között. Semmi mást nem szerettem volna, mint ennek a tisztázását, amennyire tőlem telik, egyszerűen, olvasmányosan és érthetően. Minden más, ami ezen túl mutat, egy másik cikk tárgya lehetne, de azt már nem én fogom megírni.
Hi!
2012. július 11. 15:53Annyit szeretnék hozzátenni a leírtakhoz, hogy a fibonacci sorozatnak csak a határértéke tart az aramymetszés értékéhez (1,618), amit az ókortól használtak a művészetekben, de sosem éri el annak értékét, mivel irracionális szám.
A példából is látszik, hogy 5/3=1,66 , 8/5=1,6 is csak közelítéssel tesz ennek eleget.
A fibonacci sorozatot (1202-ben)egy matematikai probléma leírására találta ki Fibonacci, vagyis vette át a hinduktól, még az aranymetszés értéke már jóval ez előtt ismert volt kb. ie.5-6.sz.
(Pheidiasz, Püthagorasz)
a+b/a=a/b ebből kifejezve jön ki az 1,618 érték, ami 1+gyök5/2
A két matematikai képlet végeredménye hasonló, de nem keverendő össze a kettő!
Szia TiSza!
2013. február 5. 17:13Örömmel olvastam a szösszenetedet, élveztem minden sorát!
Örülök, hogy ráakadtam, nem annyira az aranymetszés, mint inkább az előadás stílusa miatt:-))
(Ha esetleg köteted jelenne meg, feltétlenül szólj! Látatlanban előfizetek rá:-))
Írj sokat!
Szép fényeket!
Köszönöm, örülök, hogy tetszett!
2013. február 5. 17:24Jelent meg :-)
Megjegyzés küldése